-
- Downloads
Fig updates, hierarchihcal model to section 7.6
Showing
- analysis_and_scripts/notes.tex 70 additions, 32 deletionsanalysis_and_scripts/notes.tex
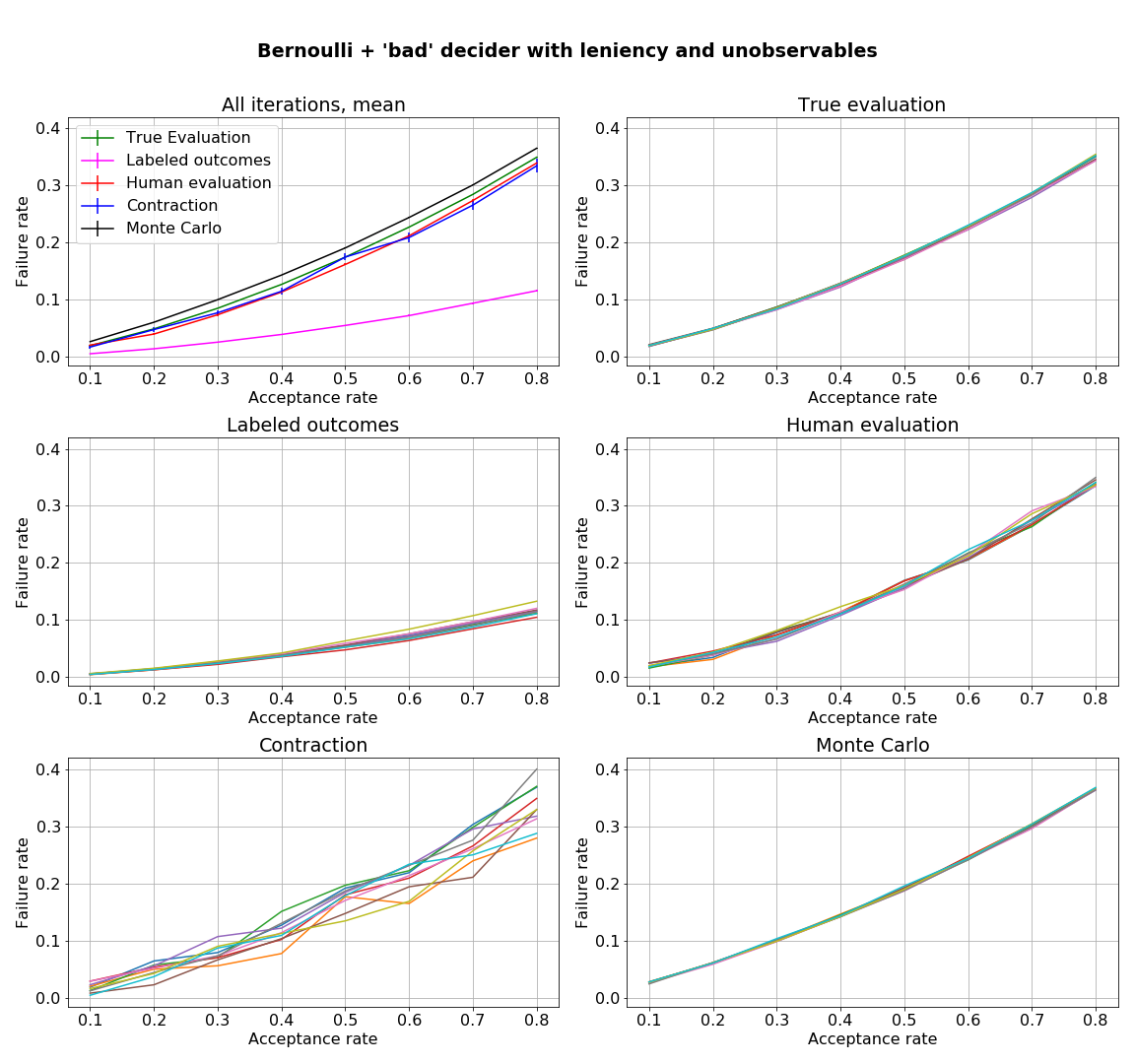
- figures/sl_diagnostic_bad_decider_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_bad_decider_with_Z.png
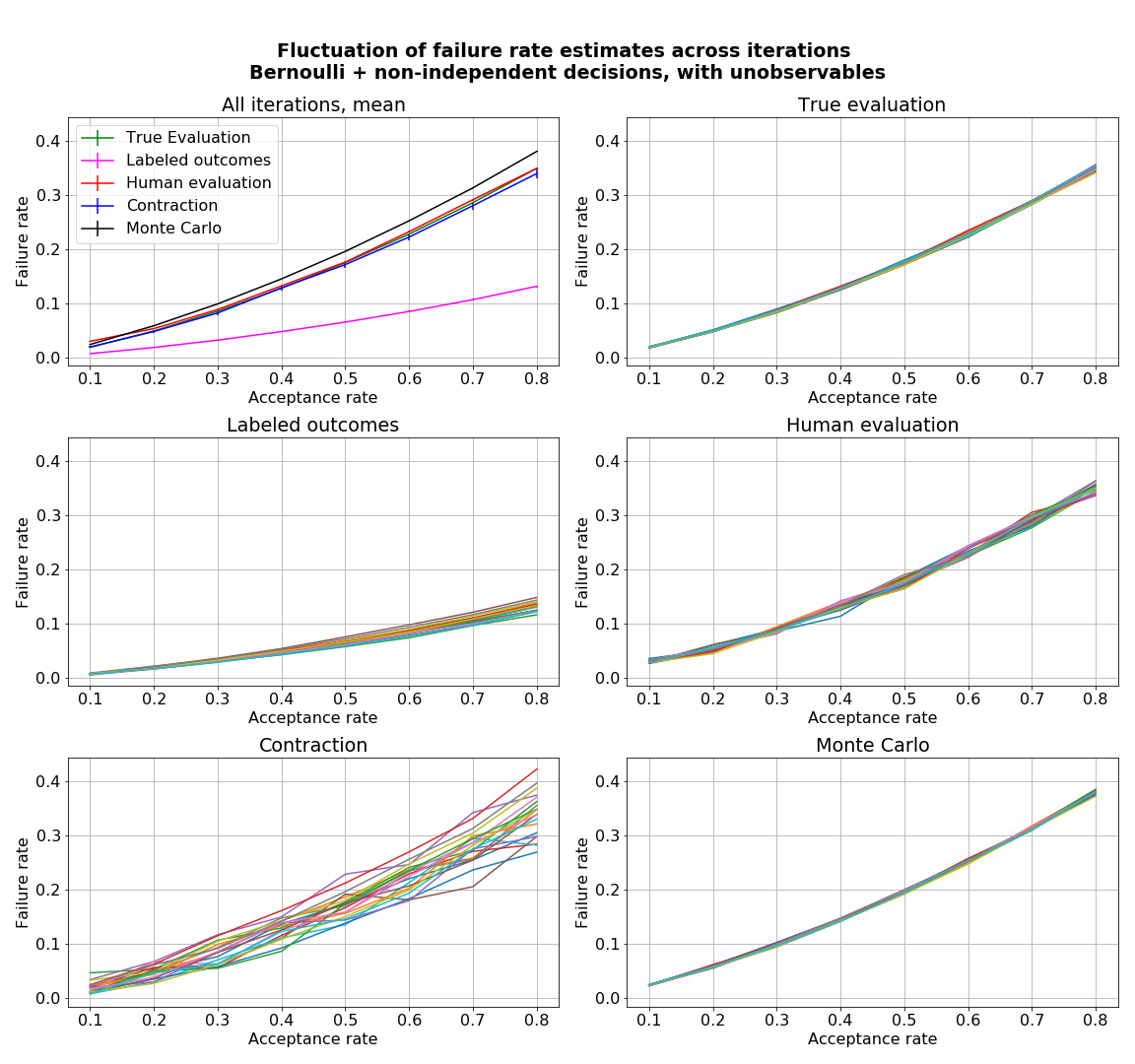
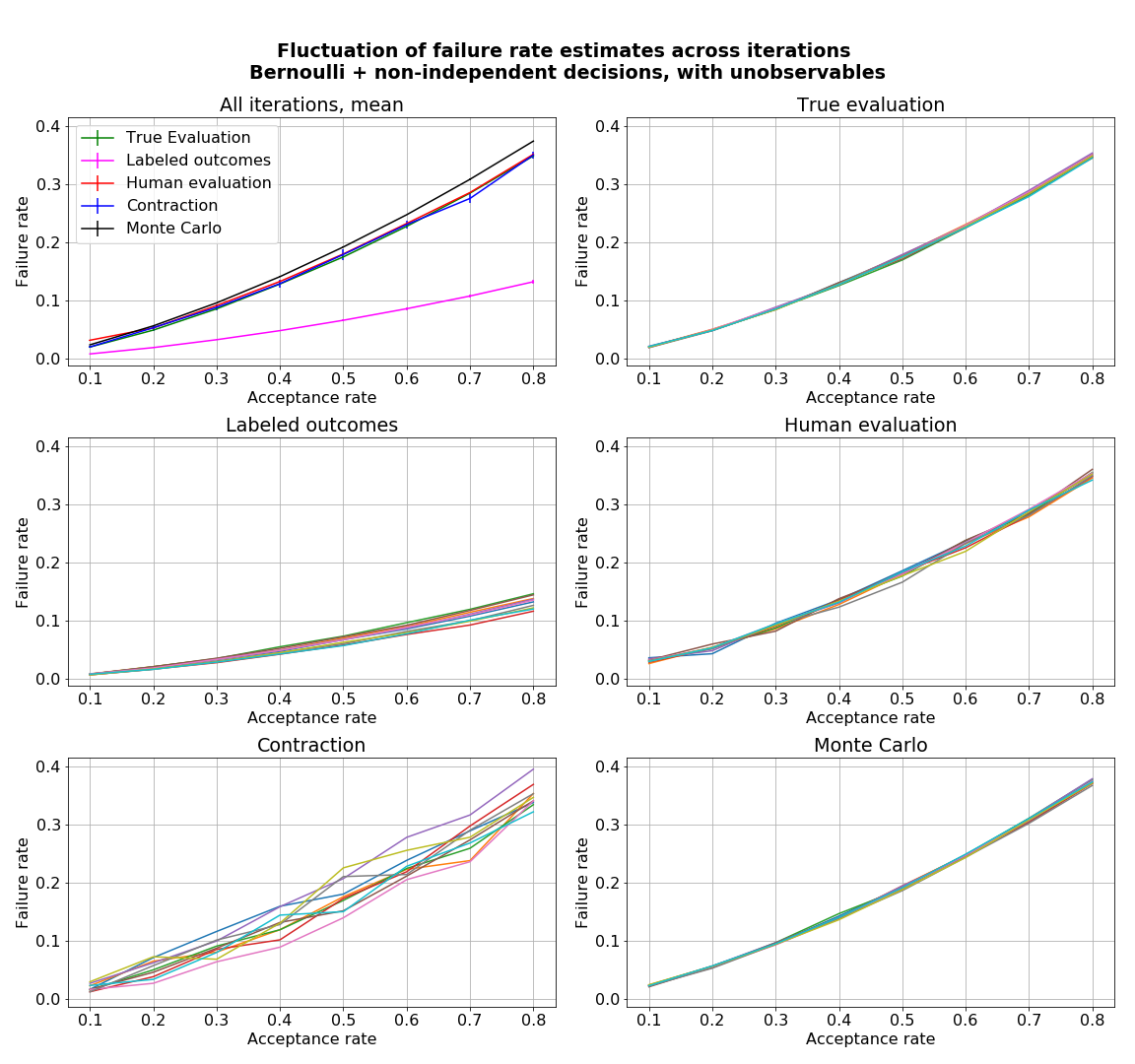
- figures/sl_diagnostic_bernoulli_batch_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_bernoulli_batch_with_Z.png
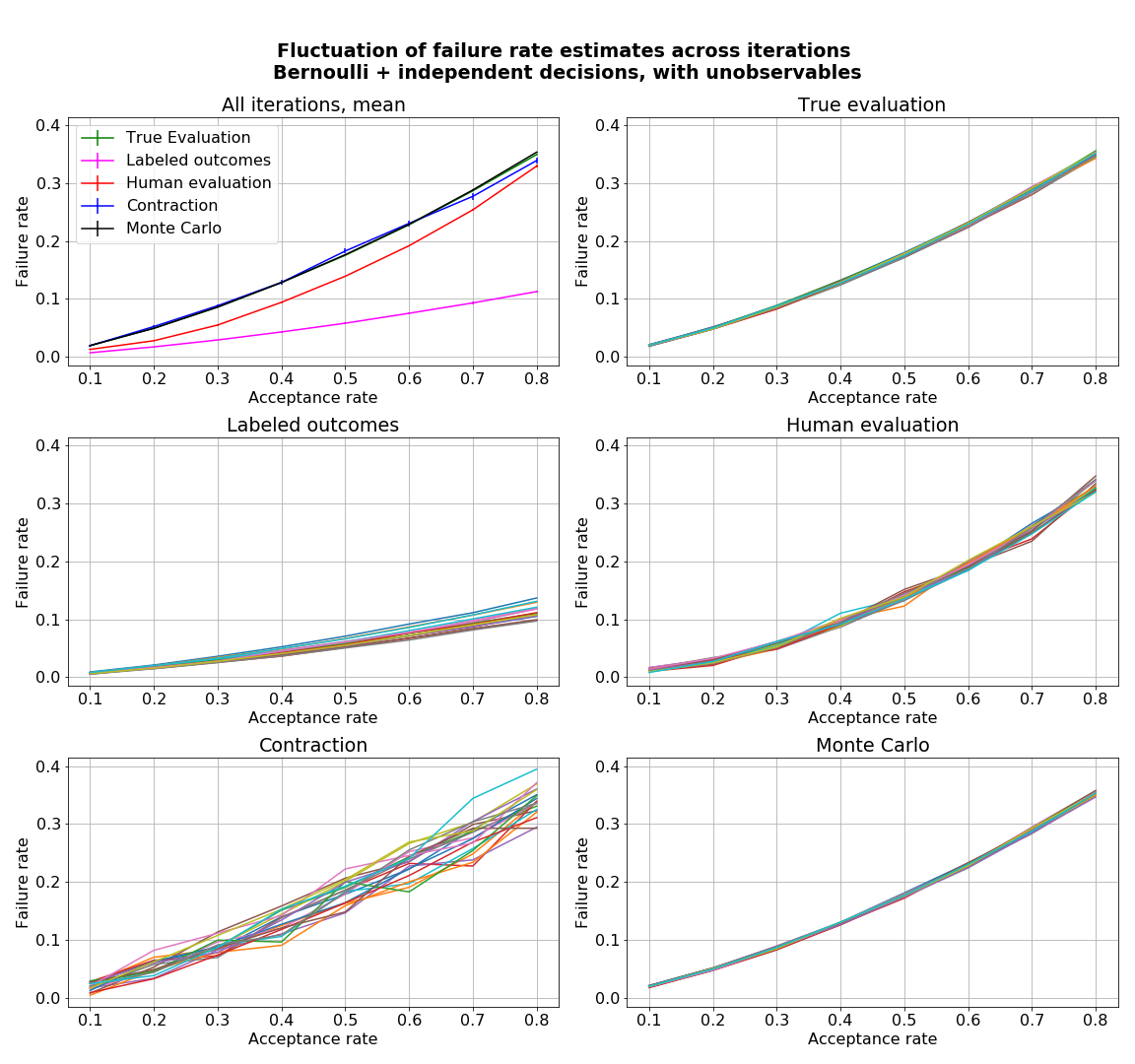
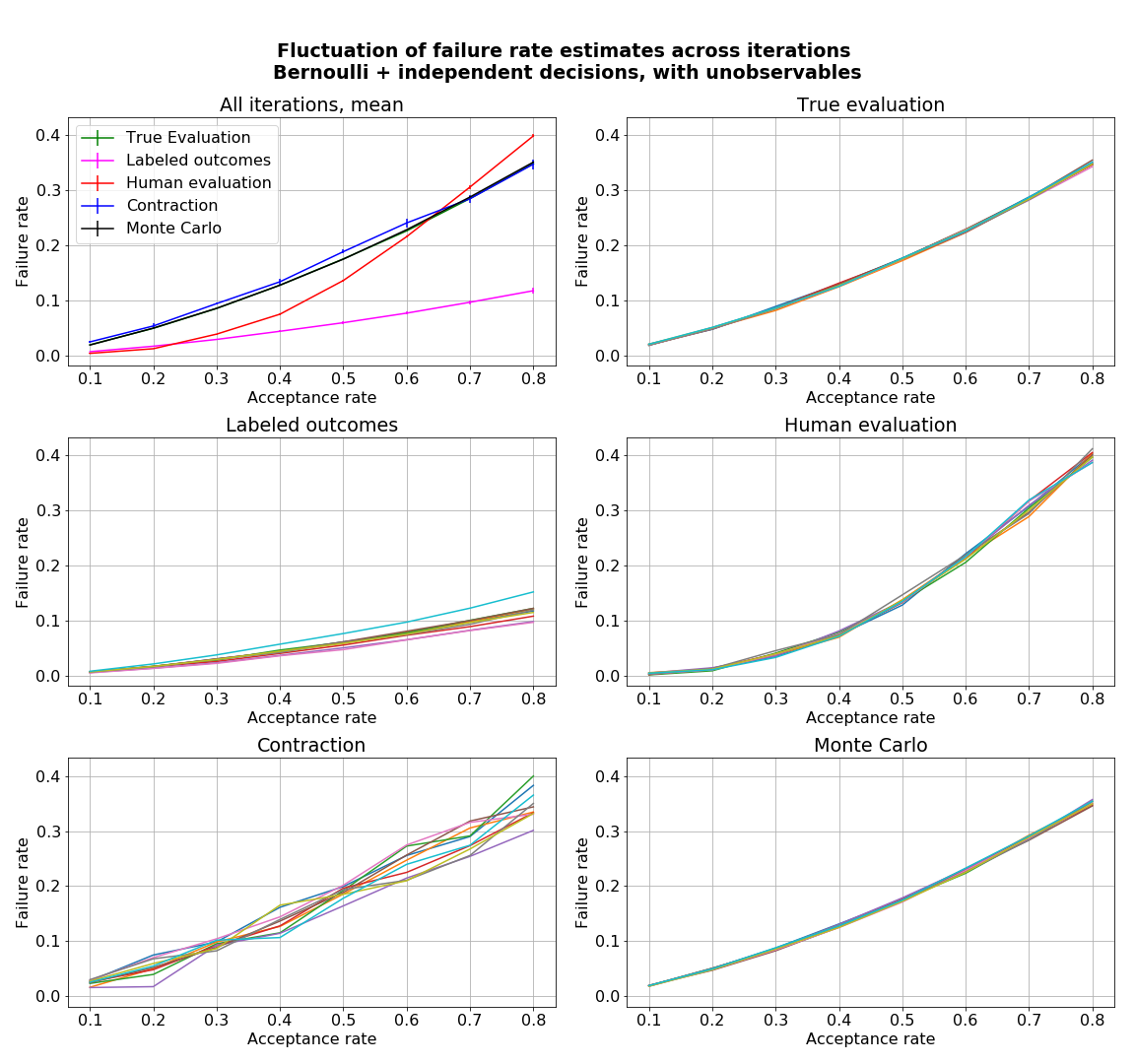
- figures/sl_diagnostic_bernoulli_independent_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_bernoulli_independent_with_Z.png
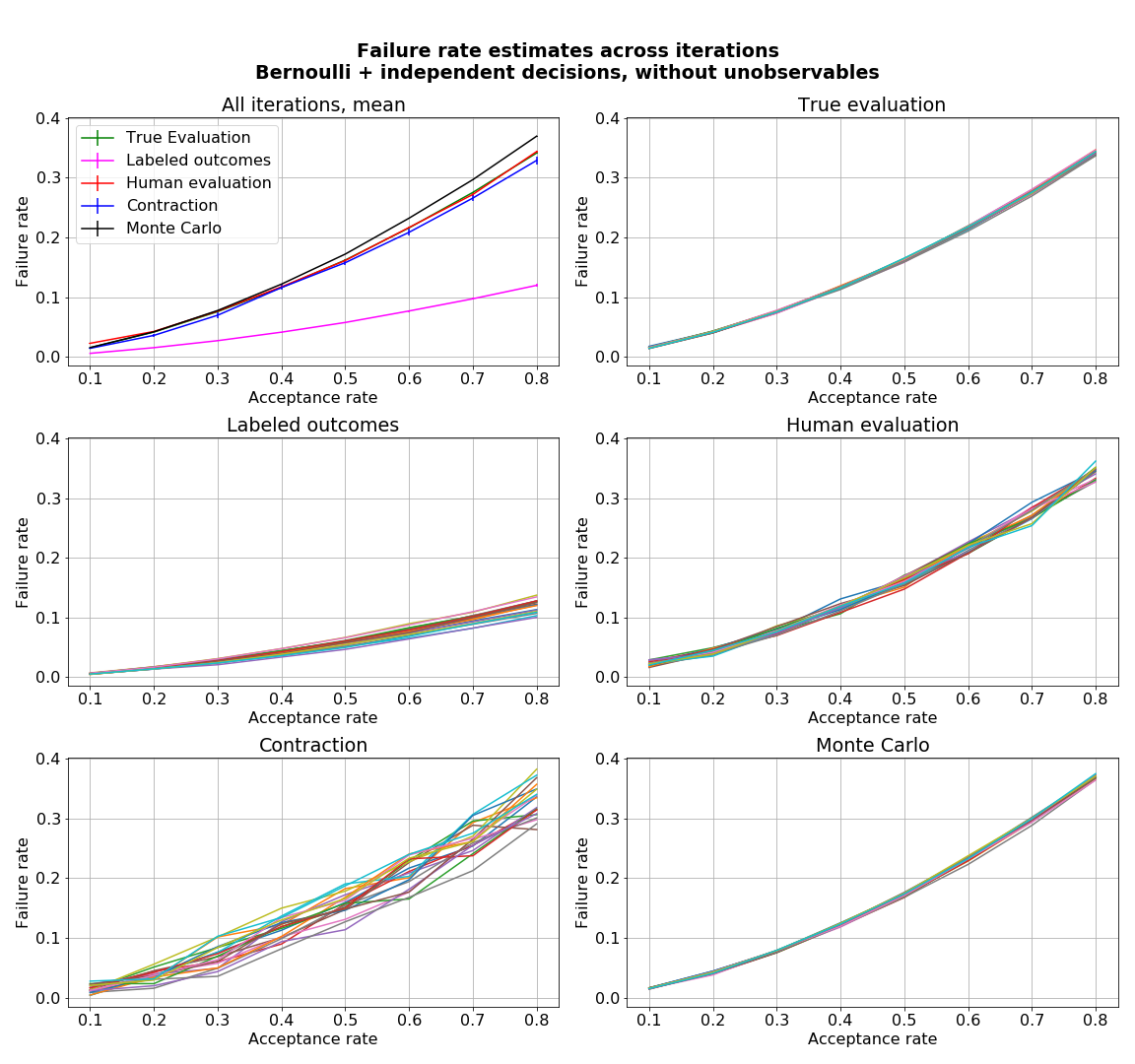
- figures/sl_diagnostic_bernoulli_independent_without_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_bernoulli_independent_without_Z.png
- figures/sl_diagnostic_biased_decider_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_biased_decider_with_Z.png
- figures/sl_diagnostic_random_decider_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_random_decider_with_Z.png
- figures/sl_diagnostic_threshold_batch_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_threshold_batch_with_Z.png
- figures/sl_diagnostic_threshold_independent_with_Z.png 0 additions, 0 deletionsfigures/sl_diagnostic_threshold_independent_with_Z.png
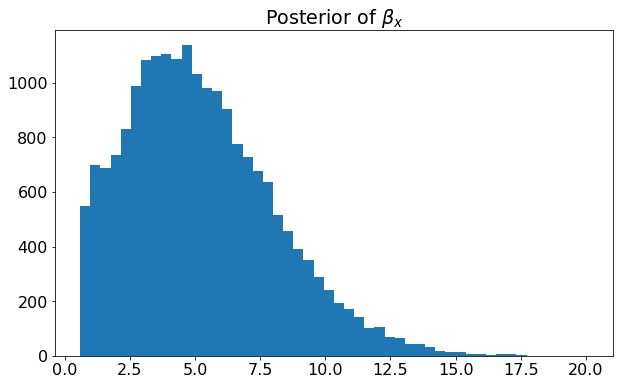
- figures/sl_posterior_betax.png 0 additions, 0 deletionsfigures/sl_posterior_betax.png
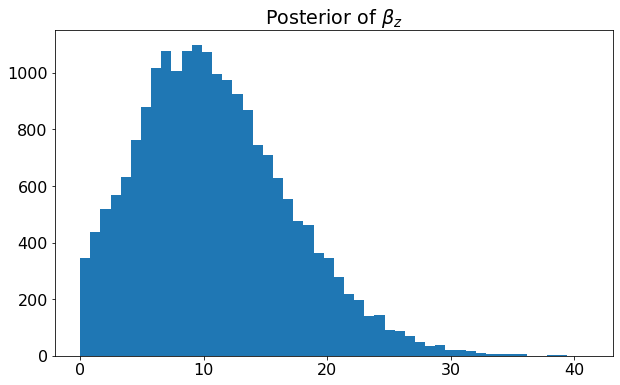
- figures/sl_posterior_betaz.png 0 additions, 0 deletionsfigures/sl_posterior_betaz.png
figures/sl_diagnostic_bad_decider_with_Z.png
0 → 100644
183 KiB
| W: | H:
| W: | H:


| W: | H:
| W: | H:


| W: | H:
| W: | H:


183 KiB
184 KiB
| W: | H:
| W: | H:


| W: | H:
| W: | H:


figures/sl_posterior_betax.png
0 → 100644
9.78 KiB
figures/sl_posterior_betaz.png
0 → 100644
8.74 KiB