-
- Downloads
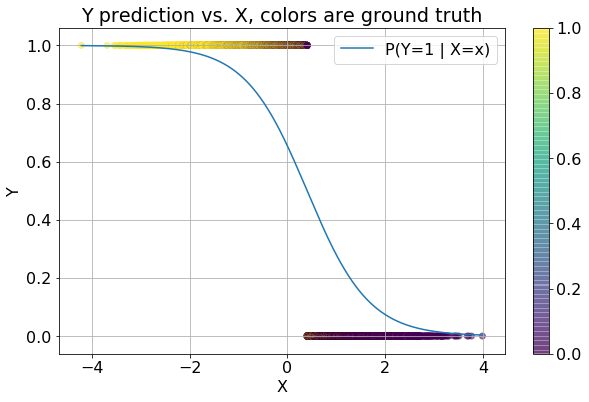
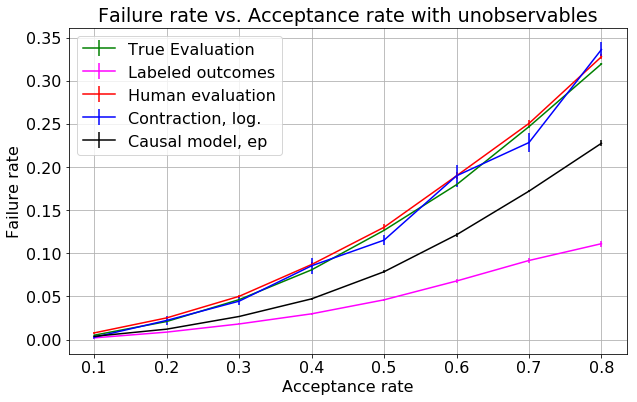
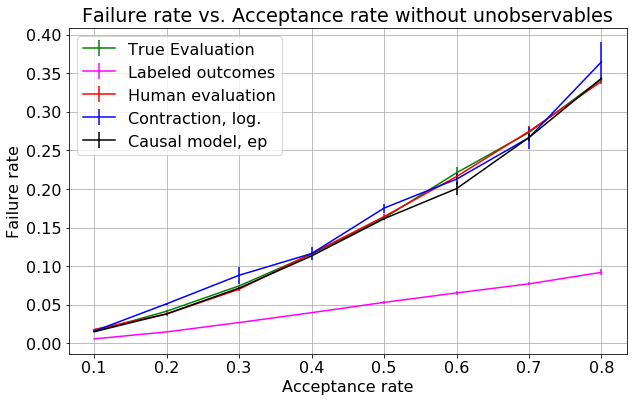
Effect of classifier and sanity check
Showing
- analysis_and_scripts/notes.tex 44 additions, 9 deletionsanalysis_and_scripts/notes.tex
- figures/sanity_check.png 0 additions, 0 deletionsfigures/sanity_check.png
- figures/sl_withZ_6iter_betaZ_1_0_randomforest.png 0 additions, 0 deletionsfigures/sl_withZ_6iter_betaZ_1_0_randomforest.png
- figures/sl_withoutZ_4iter_randomforest.png 0 additions, 0 deletionsfigures/sl_withoutZ_4iter_randomforest.png
figures/sanity_check.png
0 → 100644
29.8 KiB
53.1 KiB
figures/sl_withoutZ_4iter_randomforest.png
0 → 100644
49.4 KiB